MATRIX AND TRANSFORMATION
Explain the concept of a matrix
Definition:
A matrix is an array or an Orderly arrangement of objects in rows and columns.
Each object in the matrix is called an element (entity).
Consider the following table showing the number of students in each stream in each form.
Form
|
I
|
II
|
III
|
IV
|
Stream A
|
38
|
35
|
40
|
28
|
Stream B
|
36
|
40
|
34
|
39
|
Stream C
|
40
|
37
|
36
|
35
|
From the above table, if we enclose the numbers in brackets without changing their arrangement, then a matrix is farmed, this can be done by removing the headings and the bracket enclosing the numbers (elements) and given a name (normally a capital letter).
Nowthe above information can be presented in a matrix form as

Any matrix has rows and columns but sometimes you may find a matrix with only row without Colum or only column without row.
In the matrix A above, the numbers 38, 36 an 40 form the first column and 38, 35, 40 and 28 form the first row.
Matrix A above has three (3) rows and four (4) columns.
In the matrix A, 34 is the element (entity) in the second row and third column while 28 lies in the first row and fourth column. The plural form of matrix is matrices.
Normallymatrices are named by capital letters and their elements by small letters which represent real numbers.

Order of a matrix (size of matrix)
The order of a matrix or size of a matrix is given by the number of its rows and the number of its columns.
So if A has m rows and n columns, then the order of matrix is m x n.
It is important to note that the order of any matrix is given by stating the number of its rows first and then the number of its columns.
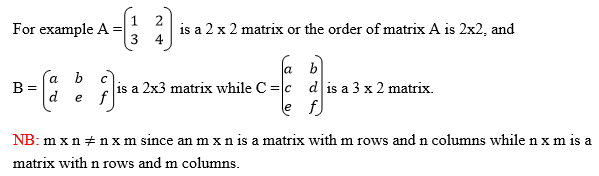
Types of matrices:
The following are the common types of matrices:-

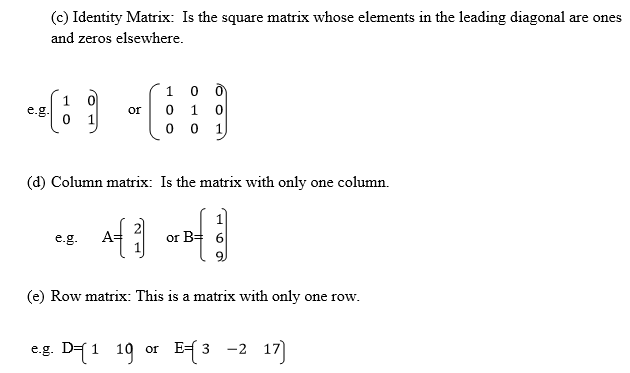
Matrices of order up to 2 X 2
Add matrices of order up to 2 X 2
When adding or subtracting one matrix from another, the corresponding elements (entities) are /added or subtracted respectively.
This being the case, we can only perform addition and subtraction of matrices with the same orders.
Example
Add matrices of order up to 2 X 2
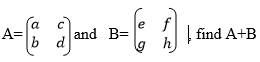
Matrices of order up to 2 X 2
Subtract matrices of order up to 2 X 2
Example
Subtract matrices of order up to 2 X 2
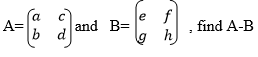
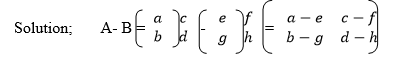
Example
Subtract matrices of order up to 2 X 2
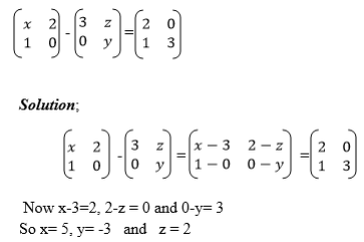
Exercise
Determine the order of each of the following matrices;
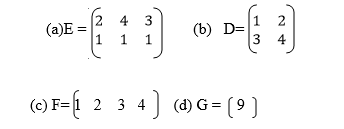
2. Given that
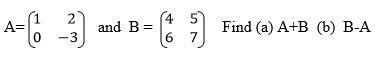
3. Given that
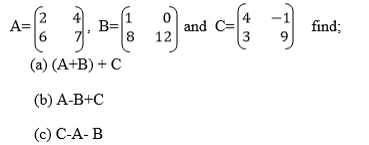
4. A house wife makes the following purchases during one week: Monday 2kg of meat and loaf of bread Wednesday, 1kg of meat and Saturday, 1kg of meat and one loaf of bread. The prices are 6000/= per kg of meat and 500/= per loaf of bread on each purchasing day
- Write a 3x2 matrix of the quantities of items purchased over the three days .
- Write a 2x1 column matrix of the unit prices of meat and bread.
5. Solve for x, y and z in the equation
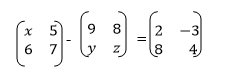
Additive identity matrix.
If M is any square matrix, that is a matrix with order mxm or nxn and Z is another matrix with the same order as m such that
M+ Z= Z+M = M then Z is the additive identity matrix.

The additive inverse of a matrix.
If A and B are any matrices with the same order such that A+B = Z, then it means that either A is an additive inverse of B or B is an additive inverse of A that is B=-A or A= -B
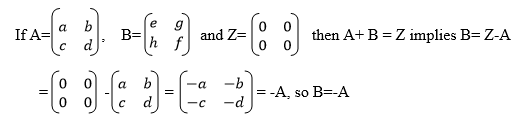
Example
Subtract matrices of order up to 2 X 2
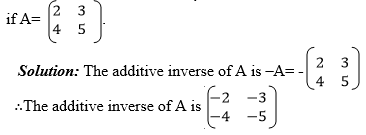
Example
Subtract matrices of order up to 2 X 2
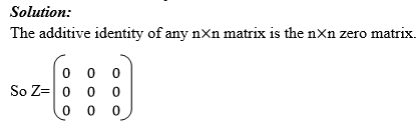
A Matrix of Order 2 X 2 by a Scalar
Multiply a matrix of order 2 X 2 by a scalar
A matrix can be multiplied by a constant number (scalar) or by another matrix.
Scalar multiplication of matrices:
Rule: If A is a matrix with elements say a, b, c and d, or
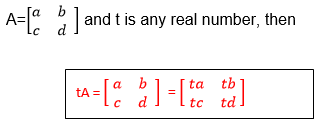
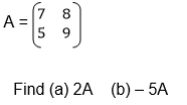
Example
Multiply a matrix of order 2 X 2 by a scalar
Solution;
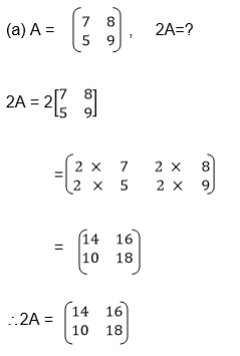
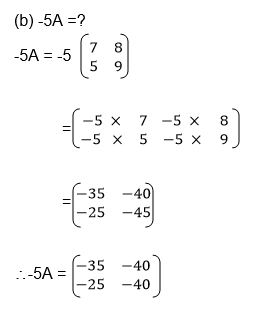
Example
Multiply a matrix of order 2 X 2 by a scalar
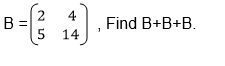
Solution;
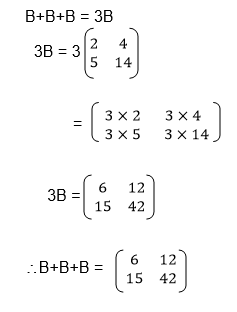
Two Matrices of order up to 2 X 2
Multiply two matrices of order up to 2 X 2
Multiplication of Matrix by another matrix:
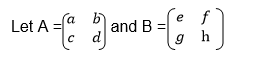
AB is the product of matrices A and B while BA is the product of matrix B and A.
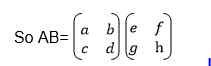
In AB, matrix A is called a pre-multiplier because it comes first while matrix B is called the post multiplier because it comes after matrix A.
Rules of finding the product of matrices;
- The pre –multiplier matrix is divided row wise, that is it is divided according to its rows.
- The post multiplier is divided according to its columns.
- Multiplication is done by taking an element from the row and multiplied by an element from the column.
- In rule (iii) above, the left most element of the row is multiplied by the top most element of the column and the right most element from the row is multiplied by the bottom most element of the column and their sums are taken:

Therefore it can be concluded that matrix by matrix multiplication is only possible if the number of columns in the pre-multiplier is equal to the number of rows in the post multiplier.
Example
Multiply two matrices of order up to 2 X 2

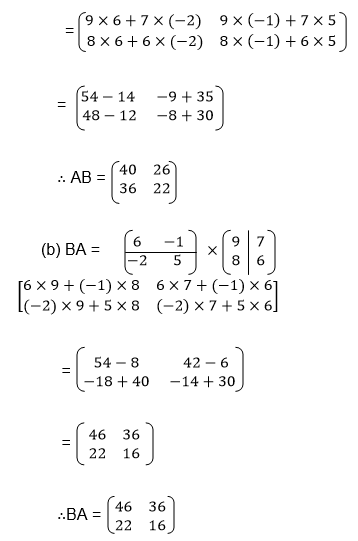
From the above example it can be noted that AB≠BA, therefore matrix by matrix multiplication does not obey commutative property except when the multiplication involves and identity matrix i.e. AI=IA=A
Example
Multiply two matrices of order up to 2 X 2
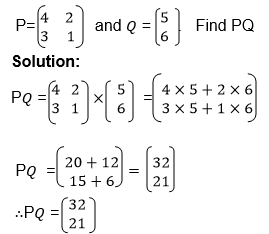
Example
Multiply two matrices of order up to 2 X 2

Product of a matrix and an identity matrix:
If A is any square matrix and I is an identity matrix with the same order as A, then AI=IA=A
Example
Multiply two matrices of order up to 2 X 2

Exercise
1. Given that A= (3 4) and

2. If,
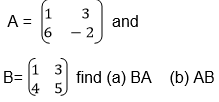
3.Using the matrices
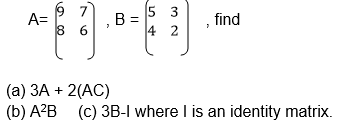
4.Find the values of x and y if
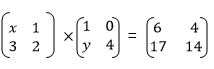
The Determinant of a 2 X 2 Matrix
Calculate the determinant of a 2 X 2 matrix
Determinant of a matrix

Now the determinant of matrix A is then defined as the difference of the product of elements in the leading diagonal and the product of the elements in the main diagonal.

Example
Calculate the determinant of a 2 X 2 matrix
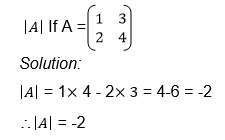
Example
Calculate the determinant of a 2 X 2 matrix
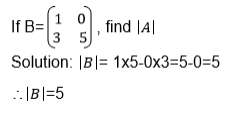
Example
Calculate the determinant of a 2 X 2 matrix

Singular and non singular matrices:
Definition:
Asingular matrix is a matrix whose determinant is zero, while non – singular matrix is the one with a non zero determinant.

Example
Calculate the determinant of a 2 X 2 matrix
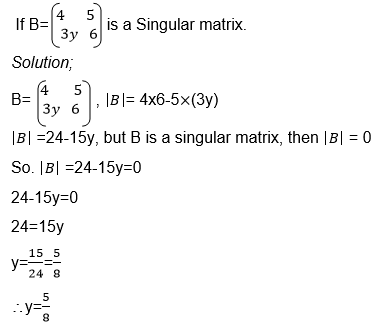
The Inverse of a 2 X 2 Matrix
Find the inverse of a 2 X 2 matrix
Inverse of matrices
Definition: If A is a square matrix and B is another matrix with the same order as A, then B is the inverse of A if AB=BA=I where I is the identity matrix.
Thus AB=BA=I means either A is the inverse of B or B is the inverse of A.
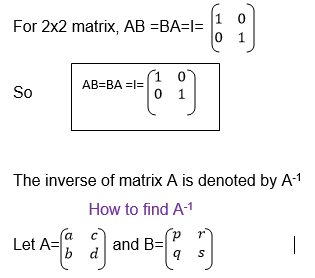
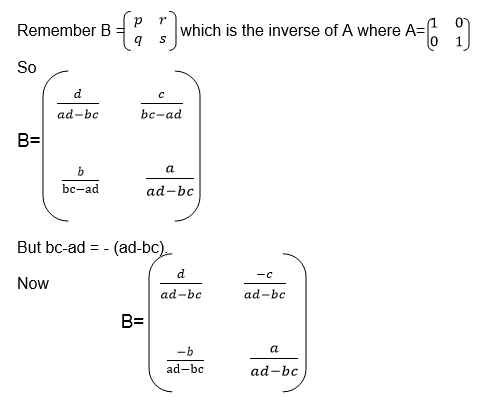
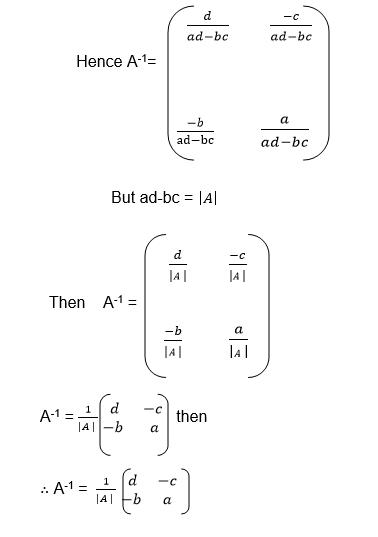
Where B=A-1, that is B is the inverse of matrix A

Since we need the unknown matrix B, we can solve for p and q by using equations (i) and (iii) and we solve for r and s using equations (ii) and (iv)

To get p proceed as follows
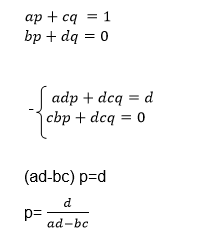
Alsoto get r and s, the same procedure must be followed:
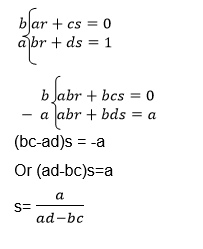
And
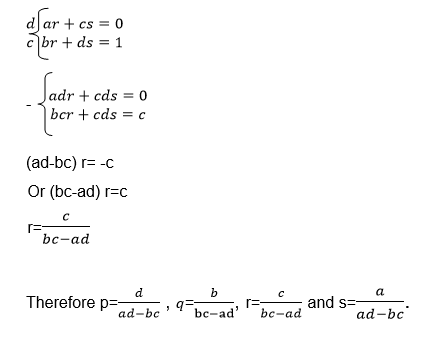
Note that, if |A|= 0, Then
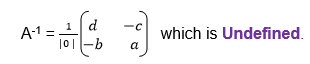
Example
Find the inverse of a 2 X 2 matrix
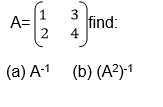
Solution:
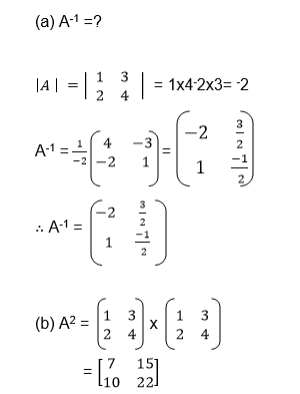

Example
Find the inverse of a 2 X 2 matrix

Exercise
1. Find the determinant of each of the following matrices.
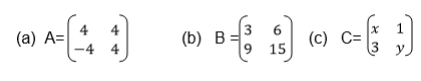
2. Which of the following matrices are singular matrices?
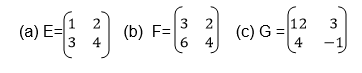
3. Findinverse of each of the following matrices.
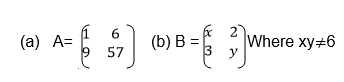
2 X 2 Matrix to Solve Simultaneous Equations
Apply 2 X 2 matrix to solve simultaneous equations
Solving simultaneous equations by matrix method:
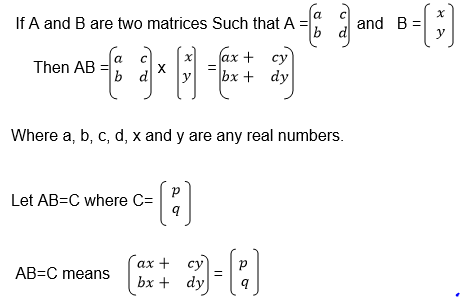
Now by equating the corresponding elements, the following simultaneous equations are obtained.

Then B= A-1×C
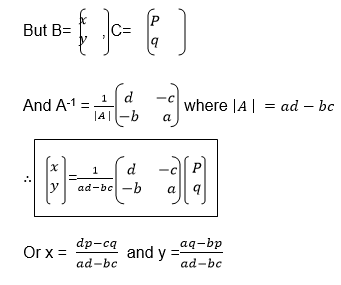
Example
Apply 2 X 2 matrix to solve simultaneous equations
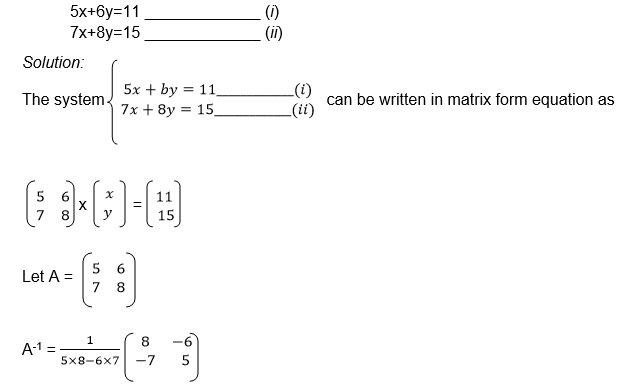
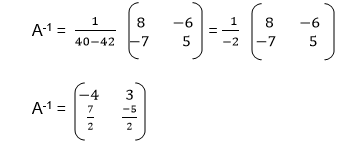
Multiplying A-1 an each side of the equation, gives,

Example
Apply 2 X 2 matrix to solve simultaneous equations

Multiplying A-1 on each side of the equation gives,

Example
Apply 2 X 2 matrix to solve simultaneous equations

Multiplying A-1 on each side of the equation gives,

Cramer’s Rule

So

Example
Apply 2 X 2 matrix to solve simultaneous equations
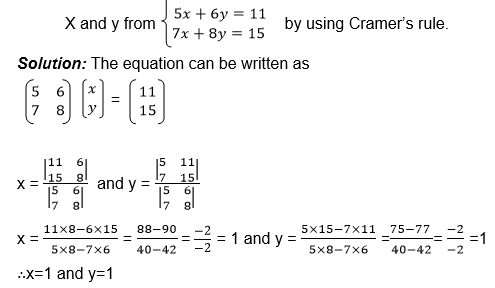
Example
Apply 2 X 2 matrix to solve simultaneous equations
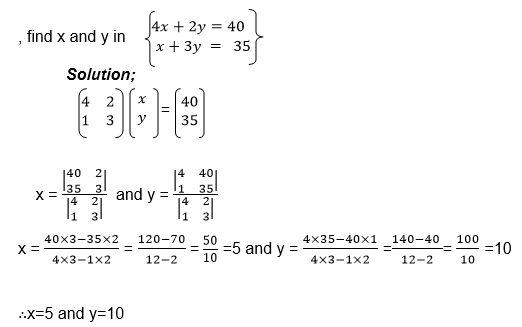
Example
Apply 2 X 2 matrix to solve simultaneous equations
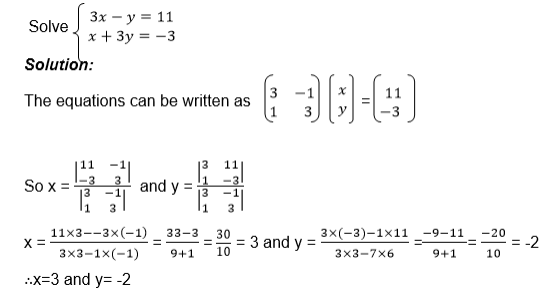
Exercise
1. Use the matrix method to solve the following systems of simultaneous equations.
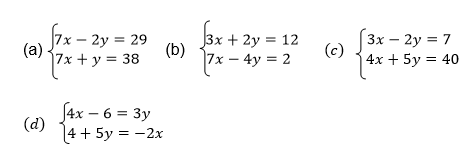
Use Cramer’s rule to solve the following simultaneous equation
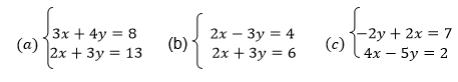
3. Whythe system of simultaneous equations

Transformations
Definition: A transformation in a plane is a mapping which moves an object from one position to another within the plane. Figures on the plane can also be shifted from one position by a transformation.
A new position after a transformation on is called the image.
Examples of transformations are (i) Reflection (ii) Rotation (iii) Enlargement (iv) Translation.
Any Point P(X, Y) into P¹(X¹,Y¹) by Pre-Multiplying (ᵡᵧ) with a Transformation Matrix T
Transform any point P(X, Y) into P¹(X¹,Y¹) by pre-multiplying (ᵡᵧ) with a transformation matrix T
- Suppose a point P(x,y) in the x-y plane moves to a point P¢ (x¢,y¢) by a transformation T,
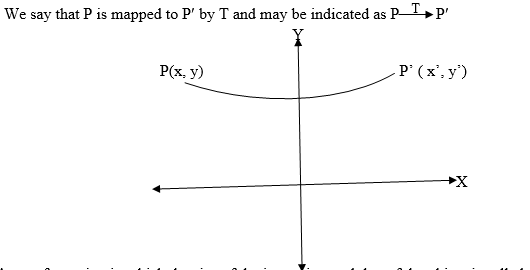
A transformation in which the size of the image is equal that of the object is called an ISOMETRIC MAPPING.
The Matrix to Reflect a Point P(X, Y ) in the X-Axis
The Matrix to Reflect a Point P(X, Y ) in the X-Axis
Apply the matrix to reflect a point P(X, Y ) in the x-axis
Reflection;
When you look at yourself in a mirror you seem to see your body behind the mirror. Your body is in front of the mirror as your image is behind it.
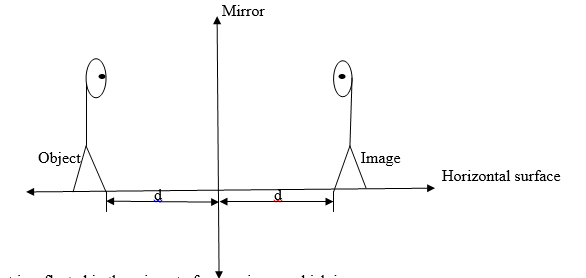
An object is reflected in the mirror to form an image which is;
- The same size as the object
- The same distance from the mirror as the object
So reflection is an example of ISOMETRIC MAPPING.
The mirror is the line of symmetry between the object and the image.
Example
Apply the matrix to reflect a point P(X, Y ) in the x-axis
Solution;
Plot point A and its image A¢ such that AA¢ crosses the x – axis at B and also perpendicular to it.
For reflection AB should be the same as BA¢ i.e. AB = BA¢
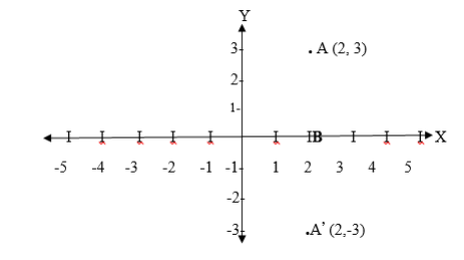
From the figure, the coordinates of A ¢ are A¢ (2,-3). So the image of A (2,3) under reflection in the x-axis is A¢ (2,-3)
Normally the letter M is used to denote reflection and thus Mx means reflection in the x – axis.
So Mx(2,3) =- (2,-3).
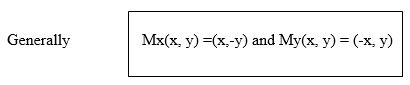
Where Mx means reflection in the x – axis and My means reflection in the y-axis.
The Matrix to Reflect a Point P(X, Y) in the Y-Axis
The Matrix to Reflect a Point P(X, Y) in the Y-Axis
Apply the matrix to reflect a point P(X, Y) in the Y-Axis
Example
Apply the matrix to reflect a point P(X, Y) in the Y-Axis
Solution:
From My (x.y)= (-x,y)
My (3 ,4 ) =( -3,4)
Therefore the image of B(3,4) is B'(-3,4) .
Reflection in the line y = x.
The line y=x makes an angle 450 with x and y axes. It is the line of symmetry for the angle YOX formed by two axis. By using isosceles triangle properties, reflection of the point (1,0) in the line y=x will be ( 0,1) while the reflection of (0,2) in the line y=x will be ( 2, 0) it can be noticed that the coordinates are exchanging positions. Hence the reflection of the point (x,y) in the line y=x is ( y,x).
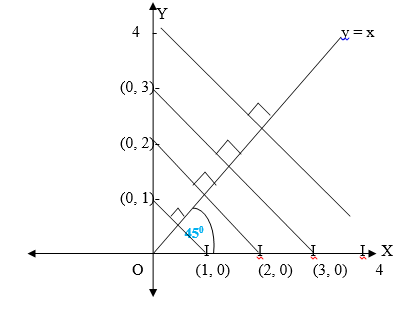
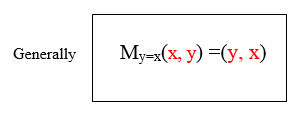
Where My =xmeans reflection in the line y=x.
Example
Apply the matrix to reflect a point P(X, Y) in the Y-Axis
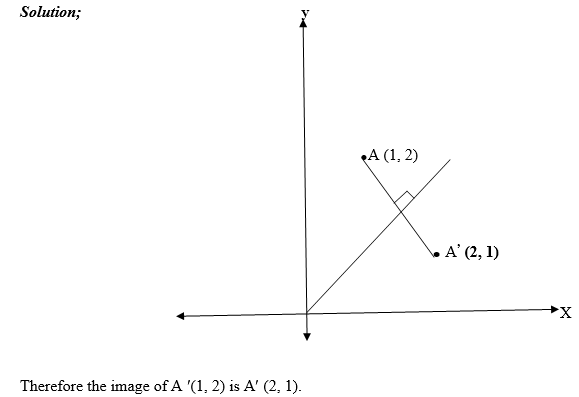
Reflection in the line y = -x
The reflection of the point B(x,y) in the line y = -x is B'(-y,-x).
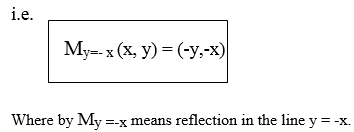
Example
Apply the matrix to reflect a point P(X, Y) in the Y-Axis
Solution;
Reflection of B in the line y=-x is B'(-4,-3). The line y=0 is the x – axis. So reflection (-4,-3) in the x-axis is (-4,3)
Therefore the image of B (3,4) is B¢(-4,3).
The image of a point P(x,y) when reflected in the line making an angleαwith positive x-axis and passing through the origin.
If the line passes through the origin and makes an angle a with x – axis in the positive direction, then its equation is y= xtanα where tanαis the slope of the line.
Consider the following diagram.
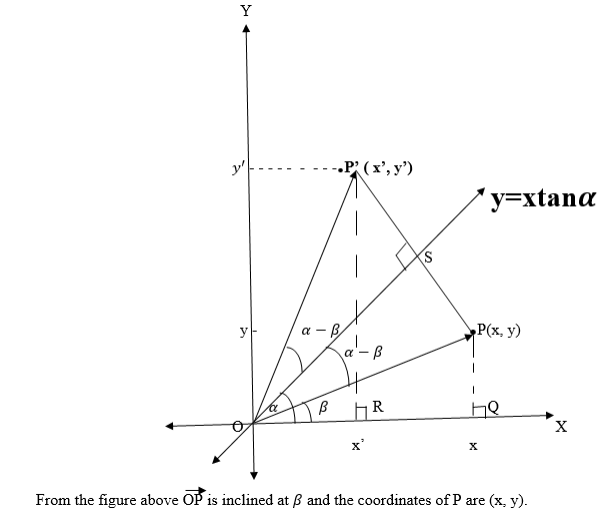

But OPQ is a right angled triangle.
So x = OP Cosβ and y = OPSinβ .
Again OP¢R is a right angled triangle and the angle P¢QR = a -β + a- β+ β, this is due to the fact that reflection is an isometric mapping.
Now the angle P¢OR = 2 a-β, then

It follows therefore that if M is a reflection in the line inclined at a, then


Example
Apply the matrix to reflect a point P(X, Y) in the Y-Axis
Example
Apply the matrix to reflect a point P(X, Y) in the Y-Axis

But the line y = 0 has 0 slope because it is the x – axis,

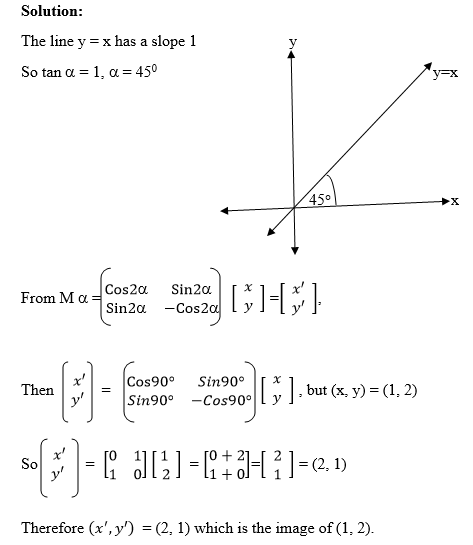
Example
Apply the matrix to reflect a point P(X, Y) in the Y-Axis
Solution:
The line y = x has a slope 1
So tan a = 1 which means a = 450
To find the image of the line y = 2x + 5, we choose at least two points on it and find their images, then we use the image points to find the equation of the image line.
Now y = 2x + 5
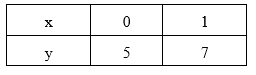
The points (0,5) and (1,7) lie on the line
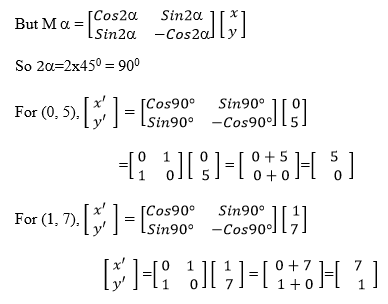
So the image line is the line passing through (5,0) and (7,1) and it is obtained as follows;
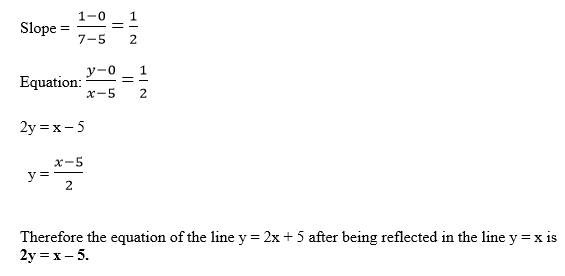
Exercise
Self Practice.
- Find the image of the point D (4,2) under reflection in the x – axis
- Point Q (-4,3) is reflected in the y – axis. Find its image coordinates.
- Reflect the point (5,4) in the line y = x
- Find the image of the point (1,2) after a reflection in the line y = x followed by another reflection in the line y = -x.
- Find the equation of the line y = 3x -1 after being reflected in the line x + y = 0.
- A Matrix Operator to Rotate any Point P( X, Y ) Through 90° 180°, 270° and 360° about the Origin
Use a matrix operator to rotate any point P( X, Y ) through 90° 180°, 270° and 360° about the Origin
Rotation:
Definition; A rotation is a transformation which moves a point through a given angle about a fixed point.
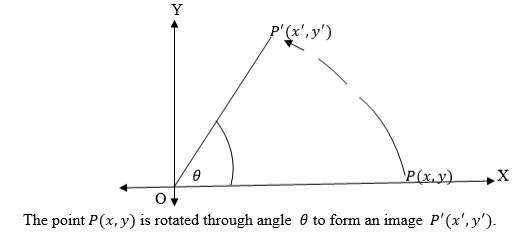
Rotation is an isometric mapping and it is usually denoted by R.
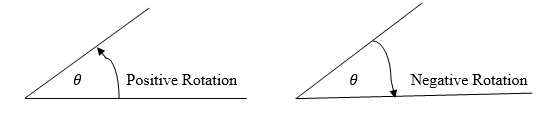
Therefore Rθ means rotation of an object through an angleθ.
In the xy plane, whenθismeasured in the clockwise direction it is negative and when it is measured in the anticlockwise direction it is positive.
Example
Use a matrix operator to rotate any point P( X, Y ) through 90° 180°, 270° and 360° about the Origin
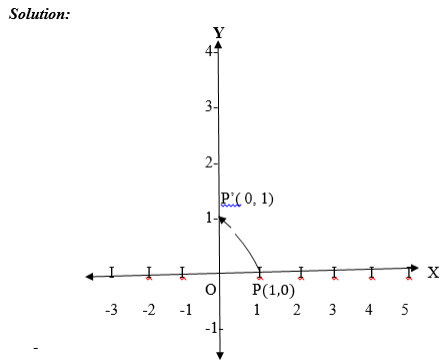
P is on the x – axis, so after rotation through 900 about the origin it will be on the y – axis. Since P is 1unit from O, P¢ is also 1 unit from O, the coordinates of P¢ (0,1) are P¢ (0,1). Therefore R 900(1,0) = (0,1).
Example
Use a matrix operator to rotate any point P( X, Y ) through 90° 180°, 270° and 360° about the Origin
Solution;
Consider the following figure,
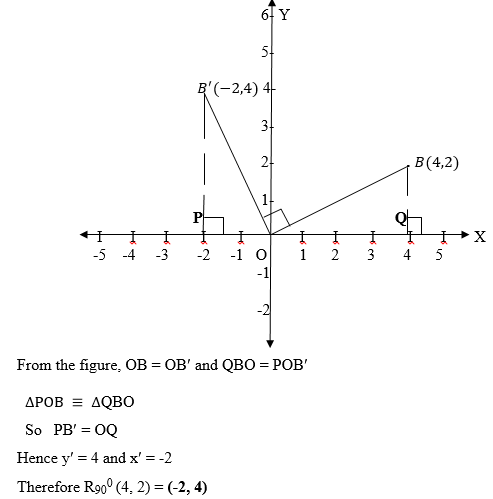
Exercise
Find the matrix of rotation through
- 900 about the origin
- 450 about the origin
- 2700 about the origin
Find the image of the point (1,2) under rotation through 1800 ant –clockwise about the origin.
Find the image of the point (-2,1) under rotation through 2700 clockwise about the origin
Find the image of (1,2) after rotation of -900.
Find the image of the line passing through points a (-2,3) and B(2,8) after rotation through 900 clockwise about the origin
General formula for rotation
Consider the following sketch,

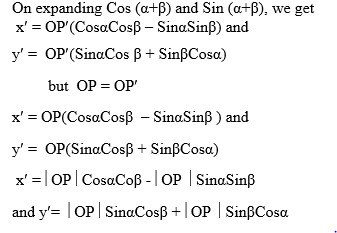

Example
Use a matrix operator to rotate any point P( X, Y ) through 90° 180°, 270° and 360° about the Origin

Therefore the image of (1, 2) after rotation through 1800 anticlockwise is (-1,-2).
Example
Use a matrix operator to rotate any point P( X, Y ) through 90° 180°, 270° and 360° about the Origin
Solution:

Therefore the image of (5,2) under rotation of 900followed by another rotation of 1800 anticlockwise is (2,-5) .
Translation
Definition: A translation is a mapping of a point P (x, y) into P' (x', y') by the Vector (a, b) such that (x', y') = (x, y) + (a, b), translation is denoted by the letter T. So T maps a point (x, y) into x', y')
Where (x', y') = (x, y) + (a, b)
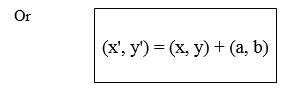
Consider the triangle OPQ whose vertices are (0,0), (3,1) and (3,0) respectively which is mapped into triangle O¢P¢Q¢ by moving it 2 units in the positive x direction and 3 units in the positive y direction
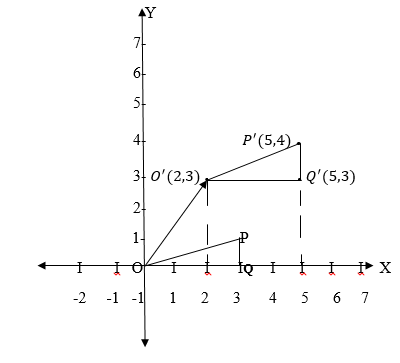

Example
Use a matrix operator to rotate any point P( X, Y ) through 90° 180°, 270° and 360° about the Origin
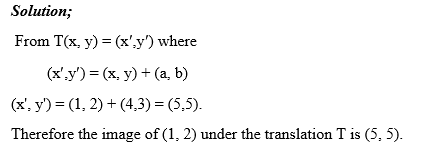
Example
Use a matrix operator to rotate any point P( X, Y ) through 90° 180°, 270° and 360° about the Origin
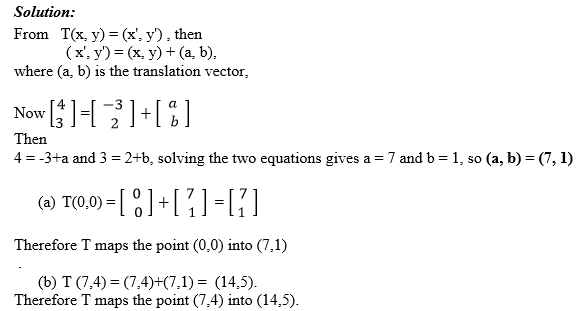
Example
Use a matrix operator to rotate any point P( X, Y ) through 90° 180°, 270° and 360° about the Origin
Solution
Given that (x, y) = (6,-6) and (x¢, y¢) = (7,16), (a, b) =?
From T (x, y) = (x, y) + (a, b) = (x', y'),
then (7,16) = (6,-6)+(a,b) which means a=7-6 = 1 and b=16+6 = 22. Therefore translation vector (a,b) = (1,22)
The Enlargement Matrix E in Enlarging Figures
The Enlargement Matrix E in Enlarging Figures
Use the enlargement matrix E in enlarging figures
Definition: Enlargement is the transformation which magnifies an object such that its image is proportionally increases on decreased in size by some factor k. The general matrix of enlargement
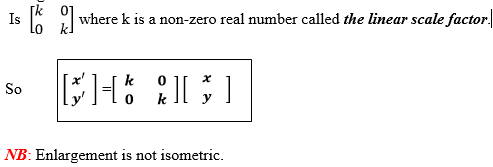
Example
Use the enlargement matrix E in enlarging figures

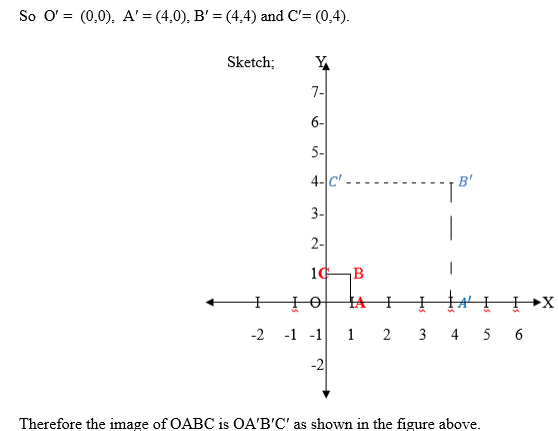
Example
Use the enlargement matrix E in enlarging figures

Example
Use the enlargement matrix E in enlarging figures

Now the images of these points are (0,3), (3,0), (0,-3), (-3,0) and other points respectively, where the centre remains (0,0) and the radius becomes 3 units.
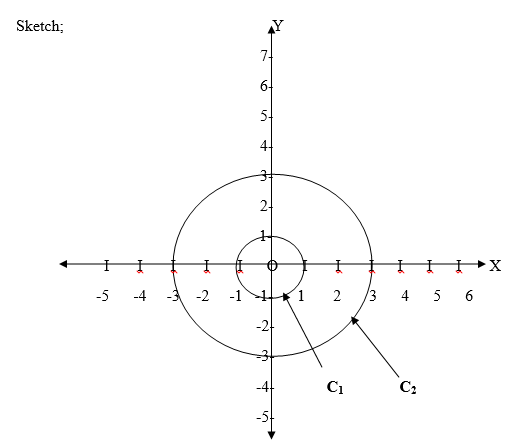
I n the figure above, the circle with radius 1 unit and its image with radius 3 units C1 and C2 respectively are shown.
Linear Transformation:
Definition:
For any transformation T, any two vectors U and V and any real number t, T is said to be a linear transformation if and only if
T(t U) = tT(U) and T (U+V) = T(U) + T(V)
Example
Use the enlargement matrix E in enlarging figures
Solution
Let U=(U1,U2) and V =(V1 , V2) be any two vectors in the plane and t be any real number
To show that R900 is the linear transformation we must show that
R900 (tU)= t R900 (U) and
R900 (U + V) = R900 (U) + R900 (V)

Therefore, since R900 (U) + R900 (V) = R900 (U+V) and R900 (tU)= t R900 (U), then R900 is a linear trans formation.
Example
Use the enlargement matrix E in enlarging figures
T(U) = (1,-2), T(V) = (-3,-1) for any vectors U and V, find
(a) T(U+ V) (b) T(8U) (c) T(3U -2V)
Solution
(a)Since T is a linear Transformation then
T( U+ V) = T(U) + T(V)
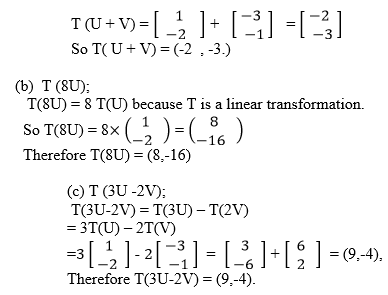
Exercise
1. If
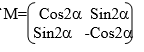
2. Is the matrix of reflection in a line inclined at angle a, U=(6,1) , V=(-1,4) and a13500, find (a) m(U+V) (b) m(2V)
If U =(2,-7) and V=(2,-3), find the matrix of linear transformation T such that T(2U)=(-4,14) and T(3V) = (6,9)
4. What is the image of (1,2) under the transformation
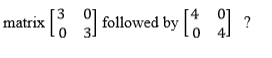
5. Given that I is the identify transformation such that I(U) =U for any Vector U, prove that I is a linear transformation.
...................end of the topic..................
Source ; shule direct (shuledirect.co.tz)
